Navigation

Navigation
NAVIGATION

NAVIGATION

Terms and Concepts

The term pilotage denotes navigation with reference only to landmarks; in contrast, dead reckoning refers to navigation using pre-calculated headings and compensating for wind to estimate groundspeed and ETA. A final expression—radio navigation—denotes navigation using electronic data from navigation aid transmitters.

Geographic co-ordinates consist of degrees longitude (meridians of longitude) and degrees latitude (parallels of latitude) to establish position, specified with degrees, minutes, and seconds. The sun travels 360° longitude in 24 hours, 15° in one hour, and 15’ longitude in one minute and 15 seconds longitude in 1 second. One nautical mile is equal to 1 minute of latitude, but note that this does not apply to longitude as the distance between degrees of longitude change.

There are two lines that can be drawn on a map: a great circle which cuts the sphere (earth) in two and represents the shortest distance between two points; a rhumb line which is a curved line that cuts all meridians at the same angle. Great circle routes are flown during long distance flights (headings have to be periodically modified).

Heading is the direction the aircraft is pointed, relative to meridians, and measured in clockwise direction, while track is the direction the aircraft travels (line) across the earth’s surface, also measured relative to meridians, in clockwise direction. In contrast, bearing is the direction of an object relative to the nose of the aircraft (longitudinal axis), or some other reference, measured in clockwise direction. A magnetic track (or magnetic heading) is the track (or heading) measured in clockwise direction from magnetic north. True track (or true heading) is the same, but measured relative to true north.

Magnetic variation is the angle between the true north (meridian) and the magnetic north (meridian) aligned with a compass. Lines on maps joining areas of equal magnetic variation are referred to as isogonic lines. A lubber line is the line on a magnetic compass that is fixed and aligned with the longitudinal axis of the aircraft. To convert true to magnetic, subtract easterly variation (“east is least”) and add westerly variation (“west is best”).

Magnetic Compass

The compass is mounted usually in acid-free kerosene that dampens movement.

There are two primary errors associated with a compass—compass deviation and magnetic dip.

Compass deviation is deviation errors of the compass caused by the aircraft’s magnetic fields. It is checked regularly as part of aircraft maintenance. Effects of deviation are minimised by corrector magnets attached to the compass housing, while the remaining deviation errors are recorded and displayed in the cockpit on the compass deviation card.

Headings flown by the pilot are corrected for magnetic variations and for compass deviation.

The compass also has errors because of magnetic dip. At the earth’s equator, magnetic lines run parallel to the earth’s surface, but towards the north and south poles, the lines “dip” towards the surface and gradually become vertical. As the needle of a compass attempts to align itself with these descending magnetic lines, it too attempts to dip. To minimize this effect, the compass is mounted as a pendulum (“pendulous mounting”), but two errors remain related to magnetic dip—Northerly Turning Error, and the Acceleration/Deceleration Error.

The Northerly Turning Error occurs during shallow turns through southerly and northerly headings. As a rule, the compass “leads” when turning from southerly headings, and “lags” when turning from northerly headings. There is approximately no turning error when turning east and west headings.

The Acceleration/Deceleration Error occurs on easterly and westerly headings whereby acceleration causes the compass to show a northerly error, and deceleration causes a southerly error. Remember this by “ANDS.” There is approximately no such error on northerly and southerly headings.

VFR Navigation Charts

There are two primary VFR charts used by pilots: VFR Navigation Charts (VNC) and World Aeronautical Charts (WAC). The VNCs have a scale of 1:500,000, and the WACs have a scale of 1:1,000,000. Both are Lambert Conformal Conic Development (type of chart) whereby the angles between the meridians and parallels will be the same on the map as they are on the ground; accordingly, for practical purposes, a straight line drawn between two points represents a great circle route. For practical purposes, when measuring the track of a line on a conic development chart, the measurement should be made at the approximate middle of the line, which provides the average track of the great circle route.

To elaborate, a great circle route drawn between two points does not intercept meridians of longitude at the same angle (since the earth is a sphere and the meridians join at the poles). In contrast to great circle routes are rhumb lines that intercept meridians at the same angle; rhumb lines would appear on a type of chart projection referred to as a Transverse Mercator Development where meridians of longitude are projected as parallel—in actuality, of course, they are not.

A third VFR chart used by pilots is the VFR Terminal Area Chart (VTA), published for larger Canadian airports (e.g., Vancouver, Edmonton, Calgary, Toronto). On VTA charts, the scale is twice that of VNC charts—i.e., 1:250,000). VTA charts are Transverse Mercator Development.

Currency

Always ensure that the map we use is current; this can be done by checking the date that appears on the front map cover near the top. On the Vancouver VNC current at the time of writing, for example, it states “13th Edition Aeronautical Information APRIL 2001.” To determine if this is the current, compare it with the current Canadian Aeronautical Charts listed on the government website—http://sat.nrcan.gc.ca/ (under Products and Services).

Highest Elevation Points

From the back cover of the map, the location of highest elevation on the chart in the Hypsometric Tints and Elevation Information—in this case, the highest point is located at 51° 22’ North Latitude, and 125° 16’ West Longitude. Note that degrees latitude and longitude are marked by black indexed lines, with longitude read horizontally, and latitude read vertically.

Additionally, note on the map that box patterns appear on the map in 30-minute intervals of longitude and latitude; these boxes are referred to as quadrangles and in the middle of each quadrangle appears a Maximum Elevation Figure in blue ink—this figure represents the highest quadrangle terrain elevation plus 328 feet (100 metres).

Airspace and the VNC

Note that all areas bounded by blue shaded boundaries (depicted right) indicate controlled airspace. Based on knowledge of Canadian airspace structure, we can be certain that controlled airspace within these boundaries always exists at 12500’ and above (this is Class B airspace and cannot be entered without a clearance). The lower base of the controlled airspace, and its class (whether C, D, or E), however, can be variable.

To find the base and its class, we must locate a depiction in blue ink somewhere within a specific boundary. Importantly, if the base of controlled airspace is not specified, the base is at 2200 feet AGL—this is the case, for example, on all airways (routes drawn on the map between radio navigation transmitters).

Finally, note that jagged blue-inked lines denote the boundary of controlled airspace with different floors.

As discussed earlier, entry into Class E low-level controlled airspace (controlled airspace below 12500’ which is not a control zone) does not require a clearance; instead entry by VFR aircraft into areas of controlled airspace is simply prohibited if the weather is below the required minimum of VFR flight.

FSS Communication

Flight Service Stations provide all in-flight information to aircraft, but of course communication with a FSS is, for the most part, possible only in VHF line-of-sight range. It is important to know where and how to contact FSS, and this is determined by two means.

Firstly, there are Remote Communication Outlets(RCO) located at various locations—they are, however, not that common. RCO depictions on the map consist of a data box joined by a line to the site, within which the location of the RCO is named. Below the RCO box is a second “half box” where the FSS to which the frequency is remoted appears. When using an RCO a pilot calls the named FSS, giving his location, and the FSS will respond on the appropriate RCO transmitter.

The second means of determining FSS communication is by examining the navigation aid data boxes. If the FSS is located in close proximity to the navigation aid, the data box for the aid appears in a thick blue-lined box; if the navigation aid appears in a box bound by a thin blue line, communication with FSS is not possible unless a “half box” appears below the data box. Where the half-box is displayed, or in the case of a thick blue-lined box, communication with the named FSS is possible using the frequencies listed above the navigation aid box.

In examining the frequencies above the data box, remember that the standard frequencies of 126.7 MHz and 121.5 MHz. can be used even though they are not displayed; they cannot be used when they appear barred (a line through the frequency) above the data box.

IFR Charts

IFR charts are quite different to VFR charts, and take a little bit of getting used to. There is virtually no depictions of land features—the one exception being large lakes and coastal shore lines, but even these are not identified by name. Instead, the great advantage of IFR charts is their application to radio navigation, and in particular to airway navigation. For every published airway, IFR charts provide navigation aid data, including frequencies and identifiers, obstacle clearance data, and data on the minimum altitude required to receive radio navigation signals. IFR charts therefore reduce the workload of the pilot, and their application in long-range commercial flight is obvious, especially when keeping in mind that legal requirements exist to keep commercial traffic on airways.

There are three types of IFR Charts: 1) Terminal Charts, which provide radio navigation data for some of the busier airports (quite similar to VTAs; 2) Enroute Low Altitude Charts, which provide radio navigation data for the en route portion of flights, up to, but not including 18000’ ASL, and, 3) Enroute High Altitude Charts, which provide similar data for the airspace at FL180 and above.

LE Charts are Lambert Conformal Conic Projection charts, and are similar to VNC Charts in that a straight line on an LE represents a great circle route.

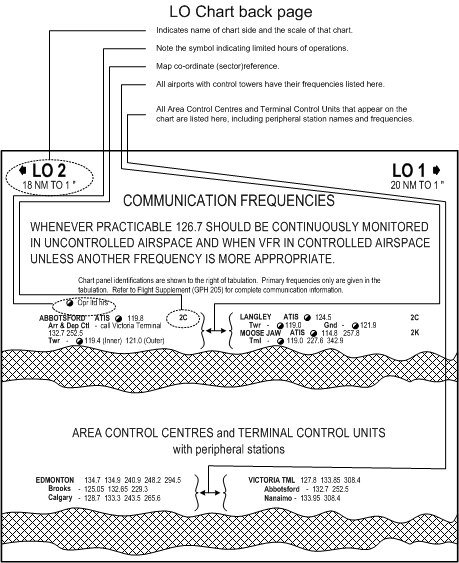
Communication

On back page of the LE are two blocks of information, the first concerning the VHF frequencies assigned to each of the major airports on the chart with control towers (including ATIS, Tower and Ground frequencies), and the second concerning the Area Control Centre and Terminal Control VHF frequencies, including peripheral station radio frequencies.

On the chart itself, the name of the applicable Area Control Centre, as well as the PAL frequencies, are identified using a boxed format. The PAL box below shows that Vancouver Centre can be contacted on 134.0 MHz., as well 381.4 MHz. (UHF).

Scale

The scale of the LE Charts vary—in the above example, for instance, the upper left and right corners of the back page show that LO 2 provides a scale of 18 NM per 1”, while LO 1is scaled at 20 NM to 1”. This variation in scale, however, is of little consequence, since all distances along airways between navigation aids and between intersections are published on the chart. In the case that a measurement is required—for example between a navigation aid and an airport—a scale bar that appears at the top and bottom of the chart can be used. Simply mark the distance on the edge of a scrap piece of paper and then position the paper next to the scale to read the distance.

Airspace

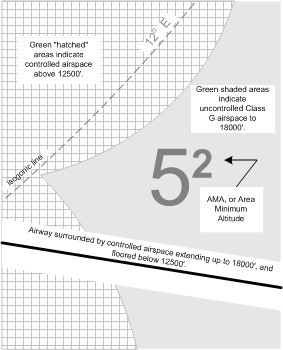
Note carefully the Legend that appears on LE charts. On the bottom right-hand corner of the Legend—under Miscellaneous—we are told that all green-shaded areas of the Chart indicate uncontrolled airspace below 18000’ ASL, while the white areas indicate controlled airspace below this altitude, including Low Level Airways, and Transition Areas. The Chart further delineates areas where controlled airspace exists above 12500’ ASL (Low Level Airways and Control Area Extensions)—all green areas patterned with white square (with green shade) hatching. Finally, note under this section is the description of isogonic lines (darker green and dashed). Note also the Area Minimum Altitudes (AMAs), which provides 2000’ clearance over the obstacle within the quadrantal (established by degrees longitude and latitude).

MOCA and MEA

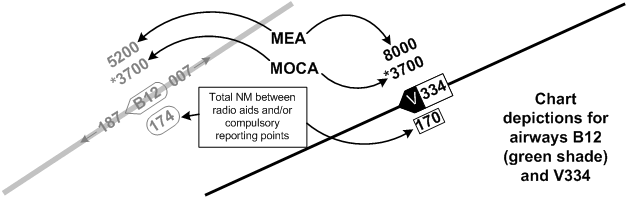
Perhaps the most important information on the LE for the IFR pilot is the MOCA (Minimum Obstruction Clearance Altitudes), which is marked with an asterisk, and MEA (Minimum En Route Altitudes), which lack an asterisk (see below).

The MOCA provides an altitude above sea level in effect between radio fixes on low level airways or air routes that meet the IFR obstruction clearance requirement for the route segment.1 Importantly, the IFR obstruction clearance requirement varies with whether or not an airway or air route is located inside or outside a Designated Mountainous Area (DMA). Outside the DMAs, the MOCA provides 1000’ clearance over the highest obstacle within 5 NM of the aircraft; inside DMAs 2, 3, and 4, this clearance increases to 1500’, and in DMAs 1 and 5 this clearance increases to 2000’.

In contrast, the MEA provides an altitude above sea level between specified fixes on airways or air routes that assures acceptable navigational coverage, and which meets the IFR obstruction clearance requirements.2 Accordingly, MEA will always be higher than MOCA.

References

1 AIM GEN 5.1 (Glossary of Aeronautical Terms)

2 Ibid.

Also note that VHF/UHF airways are depicted in black ink, while LF/MF airways are in green. You will not have difficulty determining the proper odd/even altitude to fly as the even altitude direction associated with an airway is indicated by the pointed end of the airway identification box.

The following show the relationship between MEA and MOCA as they are applied to airway segments:

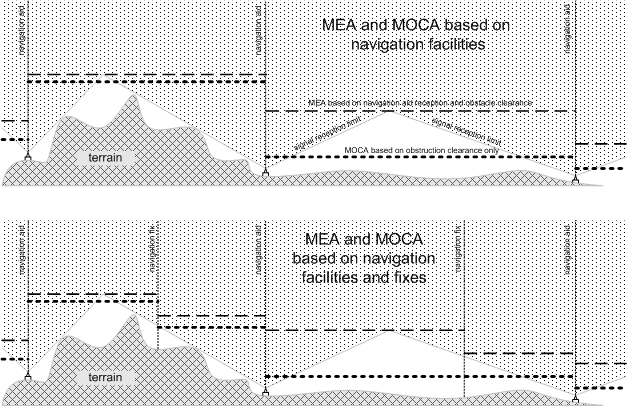
Note that each of the fixes depicted above will actually appear as an intersection on the LE chart, including the means by which the intersection is determined—i.e., DME, a radial or bearing from a neighbouring radio aid.

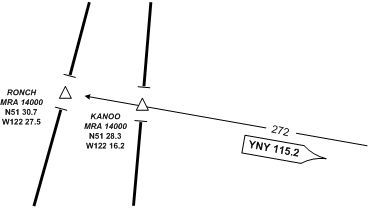
Minimum Reception Altitude

The Minimum Reception Altitude (MRA) should not get confused with the MOCA and the MEA. While the latter provides obstruction clearance data, the MRA only provides reception altitude guidance for published intersections. Specifically, the MRA is provided for specific VHF/UHF intersections and specifies the lowest altitude above sea level at which acceptable navigational signal coverage is received to determine the intersection.

Two intersections are depicted below—Ronch and Kanoo Intersections. They share the same MRA (14000’ ASL). Note that the co-ordinates for the intersections are provided, as is the radial, identifier, and frequency for the VOR used to establish the positions.

Radio Aids, Distance and Course Data

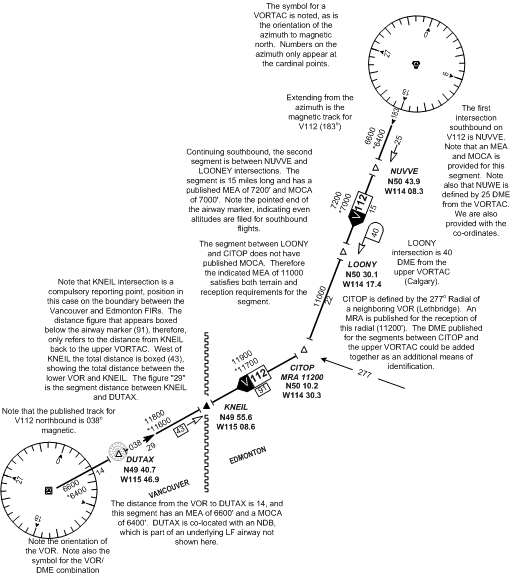
All radio Aids—i.e., NDB, VOR, VORTAC—are orientated to magnetic north in the Southern Domestic Airspace, and true north in the Northern Domestic Airspace. While the azimuths are correctly positioned, other navigation aid symbols may be positioned for sake of clarity.

The radio aid, distance and course data for the airway V112 between Calgary VORTAC and Cranbrook VOR is examined in detail to below. Note that the actual distances between symbols are only approximated for the sake of clarity.

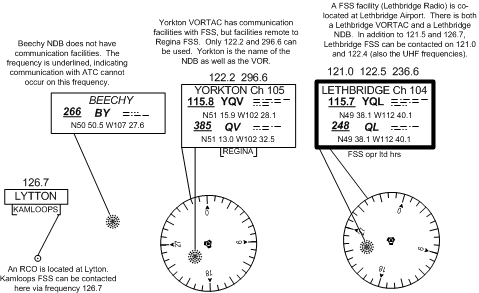
Navigation and Communication Data Boxes

The radio aid data boxes are virtually identical to the pattern used on VFR charts. A heavy line around the navigation aid data box indicates the facility is co-located with FSS. In the case a thin-lined box, FSS is not co-located with the facility. Remote FSS communication equipment is established at many radio aid sites, and these are indicated by the appearance of a sub-box below the navigation aid data box.

Standard frequencies—126.7, 121.5, and 243 MHz—are available for contacting FSS where FSS is co-located at the radio aid facility (heavy lined data boxes), unless otherwise noted. Additional frequencies used by FSS will be published above the data box, but note that the standard frequencies will not appear here—instead, it is implied that they are usable. If any of the standard frequencies are not available, they will be shown with a line through them. Note that the standard frequencies do not apply to thin-lined data boxes showing remote FSS communication; in these cases, only the frequencies published above the data boxes can be used.

Below appear three varieties.

Airport Data

The Aerodrome and Aerodrome Data depiction on IFR charts are conventional, and do not vary substantially for VFR chart references. Importantly, however, airports with published instrument approach procedures are displayed in black ink.

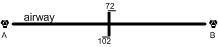
Changeover Points

Normally the radio aid used for tracking an airway is changed between the anchoring facilities at the half-way mark. Where this changeover point is different, it is marked as indicated on the right. En route from VOR A to VOR B, the VOR A is selected until the 102-NM mark is reached, and then VOR B is selected.

Course Correction Methods

Before examining navigation further, it is important to understand methods of course correction. By definition, course correction is the process of correcting the compass heading in flight owing to an adverse drifting off the original planned course. Course correction therefore entails correcting the estimations made during the pre-flight planning, owing to incorrectly forecasted upper winds, or calculation error.

The two basic methods of course correction are referred to as the double track method, which is used only during flight along first half of the course, and the opening/closing angle method, used most often during flight along the second half of the course.

Double Track Method

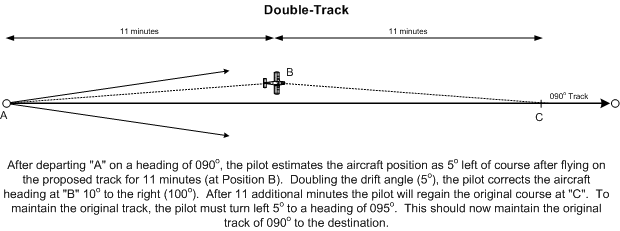
When drift error is recognized (usually at the first checkpoint), a dot is placed on the map showing the erred position of the aircraft. Using the double-track method, the opening drift angle is estimated and noted (for example, 7°). To regain the correct track, this drift angle is doubled (14°), and then added or subtracted (depending on whether drift is to the right or left of the intended track) from the heading that produced the drift error. This is the correcting heading (for example, an original heading of 090° with a drift to the left of track would result in a correcting heading of 104°). When turning to the correcting heading, the time is noted; the correcting heading is flown for the same amount of time that the erred heading was flown (i.e., the time it took to fly from the set-heading point to the point at which error was detected). When the predetermined time expires, mathematics provide that the aircraft will arrive over the original track. When the original track is recovered, the correcting heading must be adjusted: take the heading that produced the drift error, plus or minus the original drift angle (for example 104° - 7° equals 090°).

Opening-Closing Angle Method

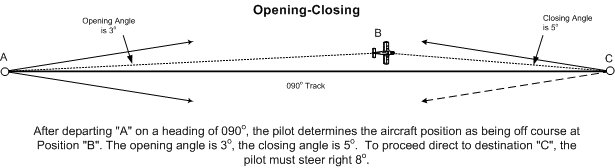
Using the opening-closing angle method, the opening and closing angles are estimated and added together; this sum is then added to or subtracted from the heading which produced the drift error, depending on whether the drift was to the left or right of the intended track. The correcting heading using this method will take the aircraft directly to the destination.

“One-in-Sixty” Rule

The One-in-Sixty Rule holds that a 1° error in course will result in the aircraft being 1 NM off course after travelling 60 miles off course.

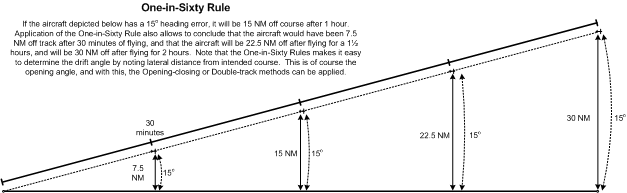
It holds, therefore, that the same aircraft was ½ miles off course after travelling 30 miles, and will be 2 miles off course after travelling 120 miles, etc. The One-in-Sixty Rule can be applied to any distance by way of ratio. For example, an aircraft is 23 miles off course after flying a 347-mile straight-line track. How many degrees is the aircraft off course? The following can be applied:

347

23 × 60

347

3.98

Therefore, the aircraft is 3.98° off course. Now let us say this aircraft has another 43 miles to go to its destination. What should be the course correction? The same ratios can be applied to the remaining destination as follows:

23 × 60

32.09

The closing angle to the destination is therefore 32.09°. Applying the opening/closing method of correction, the aircraft must turn 36° to proceed direct (4° + 32°).

ADF, VOR, and GPS Navigation Procedures

Homing and Tracking

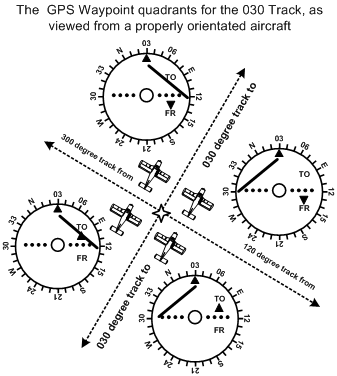
To “home” to a VOR station or GPS waypoint:

tune and identify the VOR station or GPS waypoint;
centre the CDI with OBS that provides a “to” indication;
fly a heading to maintain the track—if the CDI migrates left, you are to the right of track; if the CDI migrates right, you are to the left of track.

To intercept a pre-determined track using VOR or GPS waypoint:

tune and identify the VOR station or GPS waypoint;
select the track desired using the OBS;
orient the aircraft so that the desired track to or from the VOR or GPS waypoint is the same as the aircraft’s heading (paralleling the track);
note whether the VOR or GPS waypoint is ahead of the lateral axis of the aircraft (indicated by a “to” indication), or behind the lateral axis (indicated by a “from” indication);
if the CDI is on the right of centre, add the desired intercept angle to the current orientated heading and fly the intercept; if the CDI is on left, subtract the desired intercept angle;
when the CDI centres during the intercept, alter course to maintain the desired track.

To “home” to a station using ADF:

tune, identify, and test the NDB;1
note the relative bearing to the NDB and turn the aircraft so that the relative bearing is 360° (i.e., the magnetic heading of the aircraft equals the magnetic bearing to the NDB);
fly to maintain a relative bearing of 360°.

To intercept a pre-determined track using ADF:

tune, identify, and test the NDB;
orient the aircraft so that the desired track to or from the NDB is the same as the aircraft’s heading (paralleling the track);
note whether the bearing indicator (the needle) is indicating right or left of the longitudinal axis of the aircraft;
if the bearing indicator points to the right of longitudinal axis, add the desired intercept angle to the current orientated heading and fly the intercept; if the bearing indicator points to the right of longitudinal axis, subtract the desired intercept angle;2
if you are intercepting a track from the NDB, you slowly “pull the tail” of the bearing indicator to match the intercept angle—when the tail “opens” to match your intercept angle, you are “on track” and should now turn on course; if you are intercepting a track to the NDB, you slowly “push the head” of the bearing indicator to match the intercept angle—when the tail “opens” to match the intercept angle, again you are “on track” and should now turn on course.3

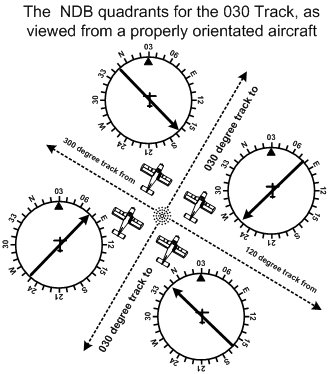
The intercept angles used are the same (unless otherwise prescribed): a 45° angle is used when intercepting a track from a station (radio navigation aid), and a 90° angle is used when intercepting a track to a station.

References

1 Unlike a VOR, the NDB signal is tested every time a new NDB is selected. If the ADF is equipped with a “test” button, this is pressed and the bearing indicator will move to the 090° relative bearing position; if the ADF does not have a test feature, move the function selector switch from the ADF position to the ANT position (the ANT position removes the directional “loop antenna” from the system, allowing only the non-directional “sense antenna” to receive the signal), and again the 090° relative bearing will be received.

2 In fact, you do not add or subtract, but instead simply glance at the ADF rotating card and read the intercept heading—presuming, of course that you have “bugged” the orientation heading. In the event of a fixed card ADF, simply transpose the bearing indication onto the heading indicator; as you turn to the intercept heading, you should see the desired track under either the 45° or 90° marker on the heading indicator.

3 This is quite tricky business and you should spend time on the ground reviewing this “tail pulling” and “head pushing” on a scrap of paper—but of course it is best seen in the air.

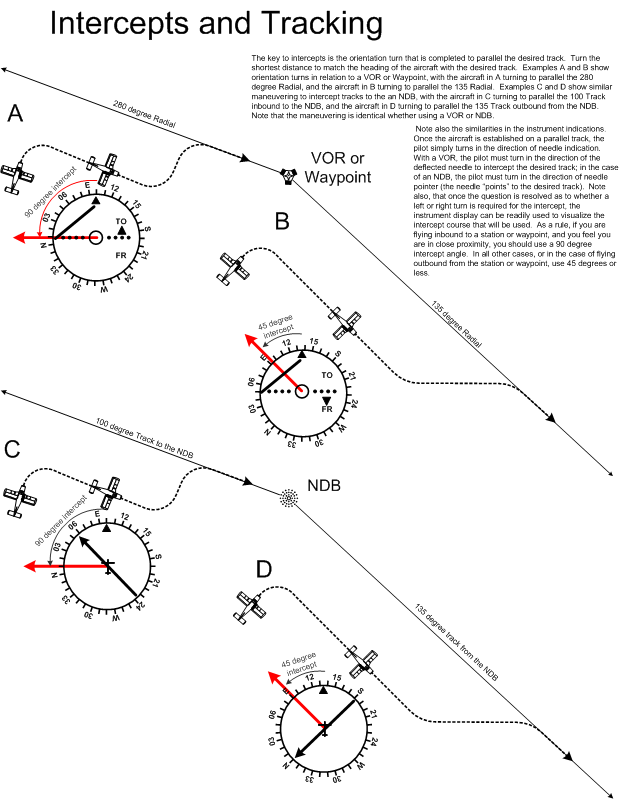
Orientation—Paralleling the Track

The key to intercepting a desired track is first paralleling the track. When you get comfortable with interceptions, you will start skipping this phase, but until you get proficient at it, always parallel the track before you intercept it. By paralleling the track, you are effectively orienting yourself and the aircraft to the ground transmitter or waypoint. Is it located in front of or behind the aircraft? Is it located to the left or to the right? With a VOR or GPS waypoint, once the track is paralleled, the information derived from the instrument display can be directly applied to your mental picture of your location—you are looking for the “To” or “From” indication to determine if it is ahead or behind, and you look for the needle deflection to determine if it is right or left. Consider the depiction below.

Navigation Formula

Relative Bearing

Magnetic bearing, sometimes simply referred to as bearing, denotes the horizontal magnetic direction to or from any point. If the magnetic bearing (or bearing) to a station is 270°, for example, this means that we are directly east of the station; similarly, if our bearing to a station is 180°, we are directly north.

Relative bearing is the position of an object relative to the longitudinal axis of the aircraft. If an object lies directly off the right wing of an aircraft, it would be considered to be at a relative bearing of 090°. If the aircraft is eastbound and an object is directly to the north of the aircraft, the object still remains at a relative bearing of 270°, even though the magnetic bearing is 360°.

An aircraft is flying on a magnetic heading of 270°. An ADF indicator shows a relative bearing to a local NDB as 010°. To proceed directly to the NDB, what magnetic heading would be flown?

Here is the formula to be used:

Magnetic Bearing = Magnetic Heading + Relative Bearing

or, MB = MH + RB

MB = 270 + 010

MB = 280

To fly to the NDB (or beacon), the pilot would fly 280°.

Now, what would happen if the magnetic heading and relative bearing, added together, equalled a value greater than 360. The solution is straightforward—simply take the sum and subtract 360. For example, an aircraft is flying a heading of 270° and the relative bearing to the station is 180°. What magnetic bearing should the pilot fly to proceed directly to the station?

MB = MH + RB

MB = 270 + 180

MB = 450

MB = (450 – 360)

MB = 090

To fly to the NDB (or beacon), the pilot would fly 090°.

A similar variation on the formula can be encountered when determining the relative bearing. To establish relative bearing by itself on one side of the equation, simply subtract MH from both sides:

MB = MH + RB

MB - MH = (MH + RB) - MH

MB - MH = RB or,

RB = MB - MH

On occasion you will find that the magnetic heading is greater than the aircraft’s magnetic bearing. A negative answer will not do, of course, but the solution is quite straight forward—simply add 360° to the magnetic bearing.

Here is an example: The aircraft’s magnetic heading is 270° and the magnetic bearing to an NDB is 180°. What is the relative bearing to the NDB?

RB = MB - MH

RB = 180 - 270

RB = (180 + 360) - 270

RB = 540 - 270

RB = 270

So, let’s see if this makes sense. The aircraft is flying westbound (i.e., from right to left across your piece of paper). The magnetic bearing to the station is 180°, so that would put the station below the aircraft at the bottom of the page (i.e., the south). What would be the relative bearing of this station with respect to the nose of the aircraft—yes, it would be directly off the left wing, or 270° measured clockwise from the aircraft’s longitudinal axis!

Time and Distance to Station

There are two formulas to be aware of which allow a pilot to determine the time or distance to an NDB or VOR station. To use the formula, the pilot must first be tracking directly to the station in question; then the aircraft is turned 90° from that heading to a perpendicular track. The pilot then notes the changes in the bearing to the station and the amount of time required to produce the bearing change.

The two equations are as follows:

Time to Station (minutes)	=	Time (seconds) required for degrees or radials change Number of degrees/radials changed

Time to Station (minutes)

Time (seconds) required for degrees or radials change

Number of degrees/radials changed

Distance to Station (NM)

TAS X Time to station in (minutes)

Applying these formulas to VORs, for example, let us assume that an aircraft is tracking inbound on the 270° Radial of a VOR. The pilot wishes to know the aircraft’s distance from the VOR station. To do this, the pilot then turns the aircraft to a heading of 360°, and starts timing. After two minutes the pilot notes that the CDI has deflected 1 ½ dots—or what is three degrees. Here comes the math:

Time to Station (minutes)

120

Time to Station (minutes)

The aircraft is 40 minutes from the VOR.

Assuming that the aircraft travels at 120 KTS TAS, the pilot then wishes to estimate the distance of the aircraft from the VOR. Here we go:

Distance to Station (NM)

120 X 40

Distance to Station (NM)=80

Now let us apply these formulas to use of NDBs. Again, the aircraft is tracking directly to an NDB and the pilot wishes to determine the exact time and distance required for station passage. Using a fixed card ADF the pilot turns 90° from the course and notes that it takes 2 minutes for the relative bearing to the NDB to change from 270° to 262°. Again, here comes the math: 120 seconds divided by 8 equals 15—the aircraft is therefore 15 minutes from the NDB. If the TAS of the aircraft is 150 KTS, 150 is multiplied by 15 to equal 2250, and 2250 is divided by 60 to equal 37.5—the aircraft is therefore 37.5 NM from the NDB.The aircraft is 80 NM from the VOR.

Finding the Sun’s True Bearing

The Sun’s True Bearing (STB) is used to provide the pilot with a means of setting the Heading Indicator (HI) independent of the compass and/or land features. By knowing the STB the pilot can point the aircraft directly in line with the sun and set the HI to the published value. Remember that in Northern Canada the compass is often rendered useless by magnetic dip and there is a lack of such features as avenues and streets, so the act of setting the HI to the STB could easily be the only means of finding your way. Of course the practice of determining STB has been eclipsed by GPS, but remember, there are no assurances that the GPS system will not be interrupted, so STB skills are still required for the commercial pilot working up north.

The STB is determined from tables published by Transport Canada Finding the Sun’s True Bearing. To extract STB from the tables, you must know your latitude and longitude and you must know your Local Civil Time (LCT). Latitude and longitude are simply derived from your position, while LCT is determined by some math. While latitude information is plugged into the STB tables, longitude is used in the math to determine LCT.

First, though, what the heck is Local Civil Time. We are familiar with standard times—Pacific Standard Time and Mountain Standard Time, for example. In the summer, these of course change to Pacific Daylight Savings Time and Mountain Daylight Savings Time. The time zones are for the convenience of civilization, but they create errors with respect to the actual position of the sun. If the time is exactly 12-noon in Pacific Time Zone, a person located in the exact middle of the province will see the sun as directly overhead. However, a person on Vancouver Island—located in western edge of the time zone—will, at the same time (noon), see the sun as lying slightly to the east of the sky’s zenith (highest point), while a person in the eastern edge of the zone—say Fernie—will at the same time see the sun slightly to the west of the zenith. So you can use standard time for an accurate determination of the sun’s bearing. In fact you have to get rid of the standards zones and instead use Local Civil Time. The fellow located in the centre of the time zone is closest to Local Civil Time. For the fellow in Vancouver, when the sun was at the zenith, this was in fact 12-noon, Local Civil Time.

The process of determining STB is outlined below according to “the book”— Finding the Sun’s True Bearing. It appears arduous to say the least, but as you read further, the shortcut method—more commonly used in the industry—is summarized. Firstly, then, here is the “long” method.

Establish for your position the whole degrees of longitude west of the Greenwich Meridian and multiply by 4; this will give you the corrective factor necessary to determine your LCT of your position.

For example, let us say that the time 2100Z and you are flying over Winnipeg where the longitude is W 82° 37’ (exclude seconds). Accordingly,

4 × 82 = 328

328 is the LCT in minutes. Now you must take this figure and convert into hours and minutes. First, determine the hours by dividing it by 60.

328 ÷ 60 = 5.47

Now we must convert 5.47 (decimal hours) hours into an hours/minutes format; to do so we now take the value .47 and multiply it again by 60:

.47 × 60 = 28.2 (or just 28 minutes)

We now have a corrective factor of 5 hours, 28 minutes.

Now, to determine LCT, we take UTC and, because we are west of the prime (or Greenwich) meridian, we subtract the corrective factor:

21:00 - 05:28 = 15:32 LCT

Now, returning to the Winnipeg example, we have determined that LCT is 15:32, and we can consult the tables contained in Finding the Sun’s True Bearing to determine STB.

Firstly, we need the latitude for Winnipeg—in this case 49° 54’ 39” (again exclude seconds). Tables are only published for every 5 degrees of latitude, so in this case we will select the tables for “50 DEGREES NORTH LATITUDE,” and from these we will select the specific table where we see (at the top of the columns) our LCT of 1532. (As reference, see the table that appears on Page 27 of Finding the Sun’s True Bearing.) The closest times that are published are 1528 and 1536. We can’t go any further unless we have a calendar date, so we shall say that the date is April 15th.

The information on the tables (for 50° North Latitude) can be summarised as follows:

Date \Hours	15:20	15:28	15:36	15:44
APR 10	242.0	243.9	245.7	247.5
APR 20	245.0	246.9	248.7	250.5
APR 30	247.8	249.7	251.5	253.3

As is the case with time, we have to extrapolate with respect to date, which can be shown as follows:

Date \Hours	15:20	15:28	15:36	15:44
APR 10	242.0	243.9	245.7	247.5
APR 20	245.0	246.9	248.7	250.5
APR 30	247.8	249.7	251.5	253.3

The middle of the top two values is approximately 245, while the middle of the lower two values is approximately 248; the best guestimate in this case (without doing math) would be 247 (mid point between 245 and 248. Accordingly, if we point the longitudinal axis of the aircraft at the sun at precisely 2100Z, we know that our true bearing will be 247°.

The Short-cut

Just note the book had you first multiply the aircraft’s longitude by 4, and then divide the product by 60. This gave you LCT in hours. Well, we can shortcut this by simply taking the longitude and dividing this by 15 (since 4/60 factors down to 1/15).

LCT (hours)

4 × 82

Is the same as

LCT (hours)